1 Frame Material Research 

Bicycle frames can be made from a variety of different materials including steel, aluminium, carbon fibre and titanium. Each of these materials has its advantages and disadvantages depending on the intended use and price range of the bicycle. The two most important physical properties of a racing bicycle frame are stiffness and density. For a bicycle to run most efficiently it must have high bottom bracket stiffness in order for the force applied by the cyclist to be transferred into forwards motion as efficiently as possible [A1]. Despite this, the frame itself must be absorbent enough that the bike can achieve a smooth and comfortable ride and light enough so that the cyclist does not have to expend unnecessary energy whilst cycling [A2]. 

Carbon fibre is one of the leading materials used in road bikes due to its high stiffness/low weight characteristics and one of the most useful aspects of it is that its material properties can be changed by varying the weave pattern and fibre direction. It has been shown that carbon fibre is at its strongest when load is being transferred parallel to the fibre direction [A3]. This is a property shared by bamboo which it has been shown is a high strength and low density naturally occurring composite material, in many ways ideally suited to bicycle frames. 

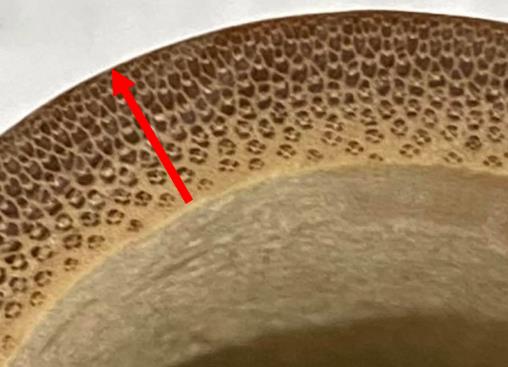
Bamboo is a composed of longitudinal cellulose fibres which exist in a matrix of lignin carbohydrate complex [A4]. These longitudinal fibres increase in density towards the circumference of the culm as can be seen in Figure 1.5.4.1 where the arrow displays the increase in fibre density from the inner diameter to the outer diameter. 

Figure 1.5.4.1: Bamboo fibre distribution

The anisotropy of the bamboo cross section results in the strength characteristics of the bamboo being largely reliant on the outer circumference of the bamboo, meaning that if necessary for weight saving applications, some inner material can be removed from the culm without significantly affecting material properties. This had potential to be used for a bamboo bike where the tube sections are manufactured using the splitting method as suggested Bamboo Bicycle Club. 

Due to bamboo being a naturally occurring, non-standardised material, the material properties can vary wildly due to variables such as moisture content, nodal length and bamboo species. With this being the case, it was recognised that experiments on bamboo samples would have to be conducted to identify the average properties of bamboo so that stress simulations could be run. 2 

14 Culms of bamboo were received from the Bamboo Bicycle Club, labelled A-N. These were first measured to identify average wall thickness, outer diameter, inner diameter and density. Out of these samples, the six highest quality culms with the least defects were chosen to be manufactured into specimens for a three point flexural bending test in order for Young’s modulus and ultimate flexural strength to be calculated. Each specimen was manufactured so that the load would be applied at the node with the supports 150mm either side of the node (300mm total length). The experiment was run to BS ISO 22157:2019 using displacement monitoring with the load being applied such that displacement of 1mm/minute would be induced. The Force-Displacement plot for the six specimens can be seen in Figure 1.5.4.2. 

Figure 1.5.4.2:Flexural bending test Force-Displacement

From Figure 1.5.4.2 it can be seen that the properties of the specimens vary and this was due to the range of diameters and wall thicknesses used as well as potential defects and anisotropies within the bamboo itself. It can also be seen that bamboo exhibits little to no plastic deformation, failure occurs once the maximum bending moment was achieved. 

From this data, Young’s modulus and Ultimate Flexural stress was calculated using equations 1-5: 

𝐼=𝜋64(𝐷𝑜𝑢𝑡𝑒𝑟4−𝐷𝑖𝑛𝑛𝑒𝑟4) Equation 1 

𝐸=𝐹𝐿348𝑌𝐼 Equation 2 

𝑀𝑚𝑎𝑥=𝐹𝑚𝑎𝑥𝐿4 Equation 3 

𝑊𝑏=𝜋(𝐷𝑜𝑢𝑡𝑒𝑟4−𝐷𝑖𝑛𝑛𝑒𝑟4)32𝐷𝑜𝑢𝑡𝑒𝑟 Equation 4 

𝜎𝑢𝑙𝑡𝑖𝑚𝑎𝑡𝑒=𝑀𝑚𝑎𝑥𝑊𝑏 Equation 5 

Where: 3 

I = Moment of inertia 

Douter= bamboo outer diameter (mm) 

Dinner= bamboo inner diameter (mm) 

E= Young’s modulus (MPa) 

F = Force (N) 

L= Support span (mm) 

Y= Vertical Displacement (mm) 

Mmax= Maximum bending moment (Nmm) 

Fmax= Maximum load achieved (N) 

Wb= Section Modulus (mm3) 

σultimate= Ultimate flexural stress (MPa) 

From these calculations an average Young’s Modulus value of 6402.93MPa was found as well as an average Ultimate Flexural Stress of 70.96MPa. 

Next a tensile test was conducted which also complied with BS ISO 22157:2019. The test specimens were all cut from the same bamboo culm to dimensions of 180mm x 8mm x 3mm to which tabs 60mm x 8mm x 1.5mm cross ply tabs were attached at each end using epoxy resin. These tabs were to be the section of the specimen the tensile machine clamped onto and so it was important that they were manufactured as precisely as possible to prevent any stress raiser features from influencing the results. The resulting specimens each had a gauge length of 60mm. 

The samples were tested on Tinius Olsen tensile test apparatus (see Appendix 5.4.1) at a displacement of 2mm/min and in order to measure strain an optical strain measurement device used. The results from the six samples can be seen in Figure 1.5.4.3. 

From these results an average Ultimate Tensile Stress of 84.34 MPa was calculated. 

Finally compressive tests were run which also adhered to BS ISO 22157:2019. Two samples were manufactured in accordance with the standard stating that the length of the sample be 10 times the thickness of the culm. The force-displacement results from the compressive testing can be seen in Figure 1.5.4.4. 

Figure 1.5.4.3:Tensile stress-strain

Figure 1.5.4.4:Compressive force-displacement

From the compressive data it was calculated that the average Ultimate Compressive Stress was 57.7 MPa. 4 

[A1]. Performance Through Stiffness and Power Transfer [Internet]. Cervelo.com. 2021 [cited 16 March 2021]. Available from: https://www.cervelo.com/en/stiffness#:~:text=Pedaling%20stiffness%20is%20also%20known,pedal%20the%20frame%20deflects%20laterally.&text=Track%20frames%20generally%20require%20more,can%20to%20be%20too%20high. 

[A2]. Shumpert M. What’s The Deal With Bamboo Bikes? [Internet]. BikesReviewed.com. 2021 [cited 16 March 2021]. Available from: https://bikesreviewed.com/fun/bamboo-bikes/ 

[A3]. Azzam A, Li W. An experimental investigation on the three-point bending behavior of composite laminate. IOP Conference Series: Materials Science and Engineering. 2014;62:012016. 

[A4]. Youssefian S, Rahbar N. Molecular Origin of Strength and Stiffness in Bamboo Fibrils. Scientific Reports. 2015;5(1).